↜ Back to index Introduction to Numerical Analysis 1
Part a—Lecture 8
In today’s lecture we use Newton’s method as a step in the backward Euler method from Lecture a4.
Report 2 is assigned.
Fill out 授業改善のための学生アンケート.
Newton’s method and the backward Euler method
We can apply Newton’s method to solve nonlinear ODEs using the backward Euler method. Recall that the backward Euler method from Lecture a4 for an ODE y'(t) = f(t, y(t)) reads as y_{n+1} = y_n + hf(t_{n+1}, y_{n+1}). The difficulty is that this is in general a nonlinear equation for y_{n+1}. We can write it as x - hf(t_{n+1}, x) - y_n = 0 for an unknown x.
Example 1. Consider the ODE
y' = -\sin y.
(This can be considered a model of an over-dampened pendulum.)
Applying the Euler method, we need to solve at each time-step y_{n+1} + h \sin y_{n+1} - y_n = 0 for y_{n+1}. There is no easy formula for this solution, but fortunately we can apply Newton’s method. Setting F(x) = x + h \sin x - y_n, we get F'(x) = 1 + h \cos x. Since \cos x is bounded, if we choose h sufficiently small F'(x) \neq 0 for any x.
Using for example x_0 = y_n as the initial guess, we perform a few iterations of Netwon’s method to approximate y_{n+1}.
! Backward Euler for y' = -sin y with Newton's method
implicit none
real x, y, h
integer n, k, nmax
h = 0.5 ! time step size for backward Euler
y = 3. ! y0: initial data
nmax = 10 / h ! number of time steps (t in [0, 10])
print *, 0., y
! loop for the backward Euler method
do n = 1, nmax
! use y_n as initial x0 for Newton
x = y
! Loop for Newton: we need very few iterations to get an
! accurate approximation if h is small.
! We could also use a stopping condition.
do k = 1, 4
! 👇 we know this is /= 0 for h small
x = x - (x + h * sin(x) - y) / (1 + h * cos(x))
enddo
! x is now an approximation of y_{n+1}
y = x
print *, n * h, y
enddo
end
Report 2 problems (final report)
The deadline is Monday, June 7, 11:00am. There is no extension possible.
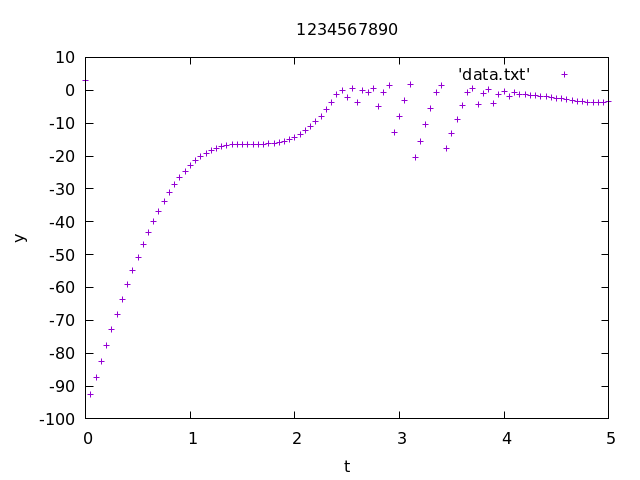
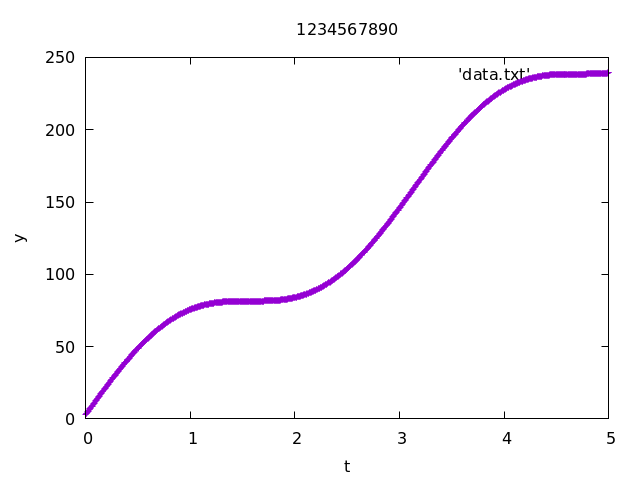
Exercise 1. Consider the ODE \left\{ \begin{aligned} y' &= 100 (\cos^2t - \exp y)\\ y(0) &= 3 \end{aligned} \right. on the time interval (0, 5). Note that \cos^2t := (\cos t)^2.
All the Fortran programs in the following small questions should read a single integer n_{\rm max} (you can assume that it is positive) and print the values of numerical solution (t_n, y_n) with h = 5 / n_{\rm max} for n = 0, 1, \ldots n_{\rm max} in the usual format:
0.00000000 3.00000000
0.500000000 -0.181777671
1.00000000 -1.16599965
...
5.00000000 -2.52394962 Implement the usual Euler method.
Plot the solution for n_{\rm max} = 100 and n_{\rm max} = 1000 (two separate plots).
Submit the plots to LMS with your student ID number as the title. 問1, 問2
Implement the midpoint method.
Plot the solution for n_{\rm max} = 1000 and n_{\rm max} = 2000 (two separate plots).
Submit the plots to LMS with your student ID number as the title. 問3, 問4
Implement the backward Euler method. At each time step, to solve the nonlinear equation for y_{n+1} use Newton’s method with at most 10 iterations and a stopping condition with tol = 10^{-3}. Initial guess for Newton’s method should be the value of the solution in the previous time step, y_n.
Submit the code to LMS. 問5
Plot the solution for n_{\rm max} = 10 and n_{\rm max} = 100 (in the same plot plot).
Submit the plot to LMS with your student ID number as the title. 問6
Discussion. You should see that for this ODE, the midpoint method requires a huge number of time steps (>1000) for the solution to not be completely wrong, while the backward Euler method gives a nice approximation already with only 10 time steps. The extra effort necessary to solve the nonlinear equation using Netwon’s method is justified.
Exercise 2. In this exercise we try to speed up solving an ODE by using a variable time step size.
Let us consider the ODE
\left\{
\begin{aligned}
y' &= \tan^{-1}(1000(t - 1))\\
y(0) &= 0.
\end{aligned}
\right.
\tan^{-1} is atan in Fortran. It is easy to see that y(2) = 0.
Plot the function f(t) = \tan^{-1}(1000(t - 1)) on the interval (0,2) using gnuplot.
Submit the plot to LMS with student ID as the title. 問7
Plot the function f'(t) on the interval (0,2) using gnuplot.
Submit the plot to LMS with student ID as the title. 問8
Write a Fortran program that reads an integer n_{\rm max} and uses the usual Euler method to solve the ODE on the interval (0, 2) with time step h = 2 / n_{\rm max} and prints the value of the numerical solution y_{n_{\rm max}} at t = 2:
Submit the code to LMS. 問9
Example. Here are outputs with n_{\rm max} = 28 and 514 for my program.
$ ./a.exe <<< 28 -0.112128347$ ./a.exe <<< 514 -6.10808562E-03Modify the program to use h that depends on f' in the following way. The program should read a real number \alpha (you can assume it is positive). At step n, use time step h_n = \alpha / (1 +|f'(t_n)|) and then update y_{n+1} = y_n + h_n f(t_n) and t_{n+1} = t_n + h_n (with t_0 = 0).
Be careful about the size of the last time step needed to reach time t = 2. There will be a time step n^* for which t_{n^*} + h_{n^*} \geq 2. If necessary, decrease the time step h_{n^*} so that t_{n^*} + h_{n^*} = 2.
The program should print y_{n^* + 1} (the numerical solution at t = 2) and n^* + 1 (the number of time steps taken).
You can assume that n^* is less than 1000000 so that your main loop can be
do n = 0, 1000000and then youexitit after condition t_n + h_n \geq 2 is satisfied.Submit the code to LMS. 問10
$ ./a.exe <<< 0.1 -1.08250305E-02 28 time steps taken$ ./a.exe <<< 0.01 -4.87289391E-04 514 time steps takenExplanation. Note that the right-hand side f(t) = \tan^{-1}(1000(t - 1)) is changing very fast only near t = 1, otherwise it stays almost constant -\pi/2 or \pi/2. It therefore makes sense to take a small time step near t = 1 and a larger time step otherwise to perform as few steps as possible. This approach is called an adaptive step size and it is very commonly used.
You can see that the solution is much more accurate with the same number of steps taken when compared to the fixed time step program in 2.
Exercise 3. Consider the ODE \left\{ \begin{aligned} y' &= y \sin t\\ y(0) &= 1 \end{aligned} \right.
Find a numerical solution of the ODE on interval (0,5) using the Runge-Kutta method of 4th order: y_{n+1} = y_n + \frac h6(k_1 + 2 k_2 + 2 k_3 + k_4). where k_1, …, k_4 are given as \begin{aligned} k_1 &= f(t_n, y_n),\\ k_2 &= f(t_n + \frac h2, y_n + \frac h2 k_1),\\ k_3 &= f(t_n + \frac h2, y_n + \frac h2 k_2),\\ k_4 &= f(t_n + h, y_n + h k_3)\\ \end{aligned} Here f(t, y) := y \sin t.
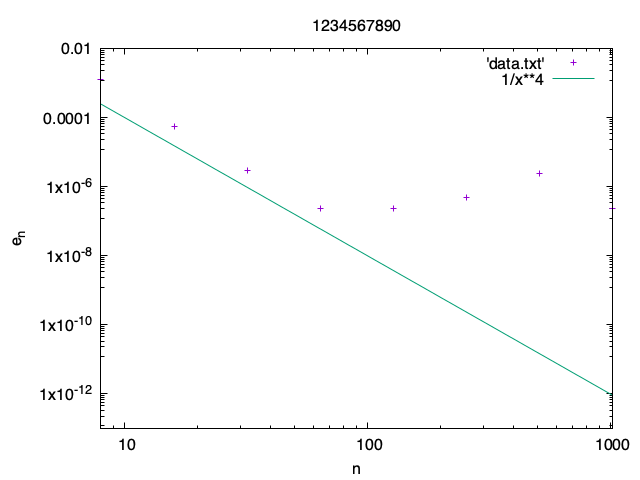
Let y^h_n denote the numerical solution at time step n for given h and n_h = 5 / h the number of time steps needed to reach t = 5. Make a program that prints the error e^h_{n_h} := |y^h_{n_h} - y(5)| for h = 5 / 2^m where m = 3, 4, \ldots 10 so that n_h = 2^m. The exact solution is y(5) = \exp(1 - \cos 5). The program should print each n_h and e^h_{n_h} on one line as usual:
$ ./a.exe 8 1.23834610E-03 16 5.67436218E-05 32 2.86102295E-06 ...Submit the code. 問11
Plot the graph of e^h_{n_h} vs. n_h for the values outputted by the program in 1. with logarithmic scale on both axes. In the same plot, plot also 1/n^4. Add labels to the axes.
Submit the plot with your student ID as the title. 問12
You should see that the error points for smaller n are on a line parallel to the graph of 1/n^4 (the method is a fourth order method) but then the error stops decreasing because the maximal precision of
realvariables is reached (about 6-7 decimal places).
Example plots
1-1. (n_{\rm max} = 100)
1-2. (n_{\rm max} = 1000)
1-3.
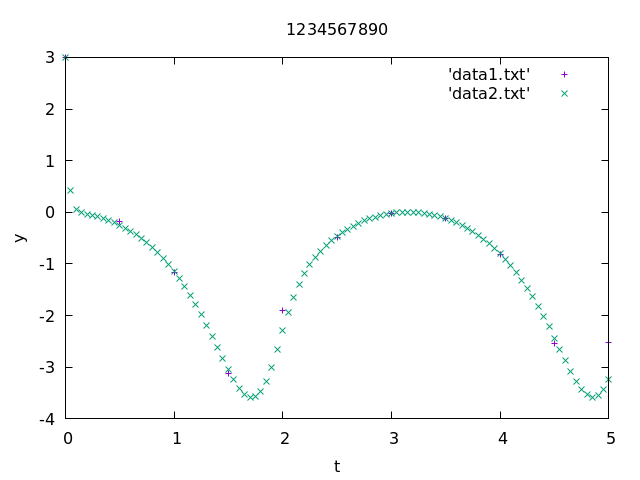
3-3.